As we all know that a computer uses binary numbers for its arithmetic as well as logical operations. Here I am going to teach you about an algebra that deals with the binary number system. This algebra is very useful in designing logic circuits used by the processors of all computer systems.

History of Boolean Algebra

In the mid 1800’s, an algebra which simplified the representation and manipulation of proportional logic was developed by the English mathematician, George Boole. It became known as Boolean Algebra after its developer’s name. Later, in the year of 1938, Claude E. Shannon, an assistance researcher in the department of electrical engineering at the Massachusetts Institute of Technology, published a thesis entitled, “A symbolic Analysis of Relay and Switching Circuits”. In Shannon’s thesis, he proposed the use of Boolean algebra in the design of relay switching circuits. The basic techniques described by him were adopted almost universally for the design and analysis of switching circuits.

Fundamental Concepts of Boolean Algebra

There are five fundamental concepts of Boolean Algebra and these are listed and discussed below.

1. Use of Binary Digits
2. Logical Addition
3. Logical Multiplication
4. Complementation
5. Operator Precedence

Use of Binary Digits

In a normal algebraic expression, a variable can take any numerical value. For example, in the expression 7a + 9b = c, we assume that a, b, and c may range through the entire field of real numbers. Since Boolean algebra deals with the binary number systems, the variable used in the Boolean equations may assume only two possible values. If an equation describing logical circuits has several variables can assume only the values 0 or 1. For example, in the equation A + B = C, each of the variables A, B, and C may have only the values 0 or 1.

Logical Addition

The symbol ‘+’ is used for logical addition operator. It is also known as ‘OR’ operator. We can define the OR operator by listing all possible combinations of A and B and the resulting value of C in the equation A + B = C. It may be noted that since the variables A and B can have only two possible values (0 or 1) so only 2² combinations of inputs are possible as shown below in the table. The resulting output values for each of the four input combinations are given in the table. Such a table is known as truth table. Thus, the table given below is the truth table of logical OR operator.

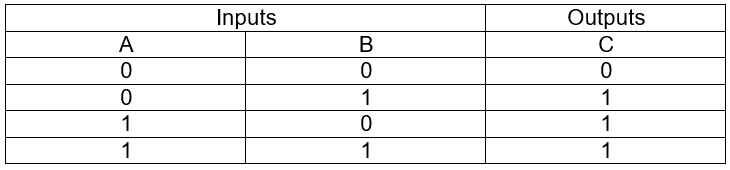
Observe that the result is 0 only when the value of both the input variables is 0. The result is 1 when any of the input variable is 1. Note that a result of 1 is also obtained when both the inputs are A and B are 1. This is the reason why the + symbol does not have the normal meaning, but is a logical addition operator.

This concept of logical addition may be extended to any number of variable. For example, in the equation A + B + C + D = E, even if A, B, C, and D all had the value of 1, the sum of the values would be 1 only. The equation A + B = C is normally read as “A or B equals C”.

Logical Multiplication

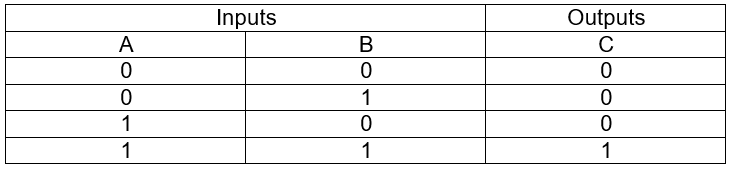
The symbol ‘.’ is used for logical multiplication operator. It is also known as ‘AND’ operator. We can again define the AND operator by listing all possible combinations of A and B and the resulting value of C in the equation A.B = C. The truth table for logical AND operator is shown below.

Observe from the truth table that the result C is equal to 1 only when both the input variables A and B are 1, otherwise it is 0. The equation A.B = C is normally read as “A and B equals C”.

Complementation

Two operations defined so far are binary operators because they define an operation on two variables. The complementation operation is a unary operation which is defined on a single variable. The symbol ’ ‘ ‘ is normally used for complementation operator. It is also known as ‘NOT’ operator. Thus, A’ means “take the complement of A” or (A + B)’ means “take the complement of A + B”.

The complement of a variable is the reverse of its value. Thus, if A = 0 then A’ = 1 and if A = 1 then A’ = 0. The truth table for logical NOT operator is shown below. A’ is read as “complement of A” or “not of A”.

Operator Precedence

Does A + B . C means (A + B) . C or A + (B . C)? The two generates different values for A = 1, B = 0, and C = 0. If we put these values we have (1 + 0) . 0 = 0 and 1 + (0 . 0) = 1. These two results are different. Hence it is necessary to define operator precedence in order to correctly evaluate Boolean expressions. The precedence of Boolean operators is as follows:

1. The expression is scanned from left to right.
2. Expression enclosed within parentheses are evaluated first.
3. All complement operations are performed next.
4. All AND operations are performed after that.
5. Finally all OR operations are performed in the end.

So according to this precedence rule, A + B . C means A + (B . C). Similarly for the expression A’ . B’, the complement of A and B are both evaluated first and the results are then ANDed. Again for the expression (A + B)’, the expression inside the parentheses (A + B) is evaluated first and the result so obtained is then complemented.

The Purpose of Boolean Algebra

1. The purpose of Boolean algebra is to facilitate the analysis and design of digital circuits.
2. It provides a conventional tool to express a truth table relationship between binary variables.
3. It provides a conventional tool to express the input-output relationship of logic diagrams.
4. It helps in finding simpler circuit for the same function.

Postulates of Boolean Algebra

The postulates listed below are the basic axioms of the algebraic structure and need no proof. They are used to prove the theorems of Boolean algebra.

Postulate 1:

1. A = 0 if and only if A is not equal to 1
2. A = 1 if and only if A is not equal to 0

Postulate 2:

1. X + 0 = X
2. X . 1 = X

Postulate 3: Commutative Law

1. X + Y = X + Y
2. X . Y = Y . X

Postulate 4: Associative Law

1. X + (Y + Z) = (X + Y) + Z
2. X . (Y . Z) = (X . Y) . Z

Postulate 5: Distributive Law

1. X . (Y + Z) = X . Y + X . Z
2. X + Y . Z = (X + Y) . (X + Z)

Postulate 6:

1. X + X’ = 1
2. X . X’ = 0

Theorems of Boolean Algebra

There are six theorems or identities in the Boolean algebra which are listed below along with their proof by using above postulates. These identities or theorem can also be proved by means of truth tables. The theorems are as follows.

Idempotent Law or Theorem One:

1. X + X = X
2. X . X = X

Proof of the first Idempotent law of Boolean Algebra:

X + X

= (X + X) . 1 [By Postulate 2]

= (X + X) . (X + X’) [By Postulate 6]

= X + XX’ [By Postulate 5]

= X + 0 [By Postulate 6]

= X [By Postulate 2]

Proof of the First Idempotent Law By Means of Truth Table:

Truth table for the first law is written below. Thus from the truth table we can see that left hand side and right hand side of the equation are same. Hence the equation is true.

Proof of The Second Idempotent Law of Boolean Algebra:

X . X

= X . X + 0 [By Postulate 2]

= X . X + X . X’ [By Postulate 6]

= X . (X + X’) [By Postulate 5]

= X . 1 [By Postulate 6]

= X [By Postulate 1]

Proof of the Second Idempotent Law By Means of Truth Table:

Truth table for the second law is written below. Since the left and the right hand sides are equal. Thus, second Idempotent law holds.

Second Theorem of Boolean Algebra:

1. X + 1 = 1
2. X . 0 = 0

Proof of the First Part of Second Theorem of Boolean Algebra:

X + 1

= (X + 1) . 1

= (X + 1) . (X + X’)

= X + X’ . 1

= X + X’

= 1

Proof of the Second Part of the Second Theorem of Boolean Algebra:

X . 0

= X . 0 + 0

= X . 0 + X . X’

= X . (0 + X’)

= XX’

= 0

Absorption Law of Boolean Algebra:

1. X + X . Y = X
2. X . (X + Y) = X

Proof of the first Absorption law of Boolean Algebra:

X + X.Y

= X.1 + X.Y

= X.(1 + Y)

= X.1

= X

Proof of the First Absorption Law by Truth Table:

This theorem of Boolean algebra can also be proved by means of truth tables. In a truth table both side of the relation are checked to yield identical result for all possible combinations of the variables involved.

In the above truth table it is proved that both sides of the Boolean identity is same as the left and right side have same values for their corresponding positions.

Proof of the Second Absorption Law of Boolean Algebra:

X . (X + Y)

= X . (X + Y) + 0

= X . (X + Y) + XX’

= X . (X + Y + X’)

= X . (X + X’ + Y)

= X . (1 + Y)

=X . 1

= X

Proof of the Second Absorption Law by Truth Table:

The above table proves the second theorem of the Absorption law of Boolean theorems.

Involution Law of Boolean Algebra:

1. (X’)’ = X

This theorem is proved by the method of perfect induction below. Note that theorem 4 has no dual since it deals with the NOT operator which is unary operator.

Theorem 5 of Boolean Algebra:

1. X.(X’ + Y) = X.Y
2. X + X’Y = X + Y

Proof of the First Part of the Theorem 5 of Boolean Algebra:

X.(X’ + Y)

= X.X’ + X.Y

= 0 + X.Y

= X.Y

Since the left hand side and right hand side of the Boolean identity are same. Thus this Boolean identity holds.

Proof of the Second Part of the Theorem 5 of Boolean Algebra:

X + X’.Y

= (X + X’).(X + Y)

= 1.(X + Y)

= X + Y

Here left and right sides are same thus this Boolean theorem also holds. These theorems can also be proved by the method of induction as above theorems have been proved.

De Morgan’s Theorems of Boolean Algebra:

1. (X + Y) = X’.Y’
2. (X.Y) = X’ + Y’

Proof of De Morgan’s Theorems

Boolean Function

A Boolean function is an expression formed with binary variables, the two binary operators OR and AND, the unary operator NOT, parentheses and equal sign. For a given value of the variables, the value of the function can be either 0 or 1.

For example, consider the equation F = A + B’C. Here the variable F is a function of A, B, and C. this is written as F = f(A,B,C) and the right had side of the equation is called an expression. The symbols X, Y, and Z are referred to as literals of this function.

The above is an example of a Boolean function represented as an algebraic expression. A Boolean function may also be represented in the form of a truth table. The number of rows in the truth table will be equal to 2ⁿ, where n is number of literals or binary variables used in the function.

The combinations of 0’s and 1’s for each row of this table is easily obtained from the binary numbers by counting from 0 to 2ⁿ – 1. For each row of the table there is a value for the function equal to either 1 or 0 which is listed in a separate column of the table.

The truth table for the function F = A + B’C is given below. We can observe from the truth table that there are 8 possible distinct combinations for the three variables. The column labelled F is either 0 or 1 for each of the combinations of the variable A, B, and C.

A	B	C	F
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	0
1	0	0	1
1	0	1	1
1	1	0	1
1	1	1	1

The question now arises here – is an algebraic expression for a given Boolean function unique? In other words, is it possible to find two algebraic expressions that specify the same Boolean function? The answer to this equation is yes. As a matter of fact, the manipulation of Boolean algebra is applied mostly to the problems of finding simpler expressions for a given expression. For example let us consider the following two functions.

F₁ = X’Y’Z + X’YZ + XY’ and F₂ = XY’ + X’Z

A	B	C	F1	F2
0	0	0	0	0
0	0	1	1	1
0	1	0	0	0
0	1	1	1	1
1	0	0	1	1
1	0	1	1	1
1	1	0	0	0
1	1	1	0	0

The representation of these two functions in the form of truth table is shown above. For the above table we find that the second function is same as the first function because both have identical 0’s and 1’s for each combination of X, Y, and Z. In general, two functions of n binary variables are said to be equal if they have the same values for all possible 2ⁿ combinations of the n literals.

Dual of A Boolean Function

In Boolean algebra there is a precise duality between the operators AND and OR and the digits 0 and 1. This important property is known as the principle of duality in Boolean algebra. The dual of a Boolean function can be found by interchanging ‘+’ with ‘.’ and ‘0’ with ‘1’, some example are elaborated below.

Example 1:- Find the dual of the Boolean function F = A‘ + B‘?

Solution:- Here the Boolean function is as F = A’ + B’. The dual of the function is found by interchanging only AND operator (+) and OR operators (.). Hence the dual of the Boolean function is as G = A’.B’ where G denotes the dual of the Boolean function.

Example 2:- Find the dual of the Boolean function F = (A‘ + B‘).(A + C).(B + C‘)?

Solution:- The Boolean function is F = (A’ + B’).(A + C).(B + C’). Now the dual of the function G = (A’.B’) + (A.C) + (B.C’) here G is the dual of the Boolean function.

Example 3:- Find the dual of the Boolean function F = (X‘.Y.Z) + (X.Y‘.Z) + (X.Y.Z‘) + (X.Y.Z)?

Solution:- The Boolean function F = (X’.Y.Z) + (X.Y’.Z) + (X.Y.Z’) + (X.Y.Z). The dual of the Boolean function F is given as: G = (X’ + Y + Z).(X + Y’ + Z).(X + Y + Z’).(X + Y + Z) where G is used to denote dual of the function.

Example 4:- Find the dual of the Boolean function F = A + A.B + A‘.C?

Solution:- The Boolean function is F = A + A.B + A’.C. The dual is G = A.(A + B).(A’ + C) where X is the dual of the Boolean function G.

Complement of a Boolean Function

The complement of a Boolean function F is F’ and is obtained by interchange 0’s for 1’s and 1’s for 0’s in the truth table that defines the function.

F = XY’ + X’Z

X	Y	Z	F	F’
0	0	0	0	1
0	0	1	1	0
0	1	0	0	1
0	1	1	1	0
1	0	0	1	0
1	0	1	1	0
1	1	0	0	1
1	1	1	0	1

Algebraically, the complement of a function may be derived through De Morgan’s Theorems whose generalized forms are as follows:

(A₁ + A₂ + A₃ + …… + A_n)’ = A’₁.A’₂.A’₃ …… A’_n

(A₁.A₂.A₃ …… A_n) = A’₁ + A’₂ + A’₃ + …… + A’_n

These theorems state that the complement of a function is obtained by interchanging the OR and the AND operators and complementing each literal. The method is illustrated below through an example.

Example1:- Find the complement of the function F = A‘B‘ + AB?

Solution:- Applying De Morgan’s theorem as many times as necessary, the complement of the Boolean function is as obtained. Let F’ denotes the complement function of the function F.

F’

= (A’B’ + AB)’

= (A’B’)’ (AB)’

= [(A’)’ + (B’)’] (A’ + B’)

= (A + B) (A’ + B’)

This is the required result. Let us take another example to have better understanding of the complementing operation.

Example2:- Find the complement of the function F = AB + (A‘B‘)(BC + B‘C‘)?

Solution:- As in the above problem we have used De Morgan’s theorem repeatedly we also apply them here.

F = AB + (A’B’) (BC + B’C’)

F’ = [AB + (A’B’) (BC + B’C’)]’

F’ = (AB)’ [(A’B’) (BC + B’C’)]’

F’ = (A’ + B’) [(A’B’)’ + (BC + B’C’)’]

F’ = (A’ + B’) [(A + B) + (BC)’ (B’C’)’]

F’ = (A’ + B’) [(A + B) + (B’ + C’)(B + C)]

F’ = (A’ + B’) (A + B) + (A’ + B’) (B’ + C’)(B + C)

This is the required complement of the above Boolean function.

Minimization of A Boolean Function

When a Boolean function is implemented with logic gates, each variable in the function designates an input to a gate and each term of the function is implemented with a gate. Thus for a given Boolean function, the minimization of the number of variables and the number of terms will result in a circuit with less equipment.

To find simpler circuit, one must know how to manipulate Boolean functions to obtain equal and simpler expressions. What constitutes the best form of Boolean functions depends on the particular application. However, we will give consideration only to the criterion of equipment minimization which is achieved by literal minimization.

Minimization of a Boolean function can be achieved by two simple ways. These two methods are as:

1. By using Boolean theorems and postulates.
2. By using Map Simplification.

Here, we will go through the first method. Let us take an example to understand the process. 

Example 1:- Simplify the following algebraic expression using Boolean algebra? done

F = XY’Z + X’Y’Z + XYZ

Solution:-

F

= XY’Z + X’Y’Z + XYZ

= XY’Z + XYZ + X’Y’Z

= XZ(Y’ + Y) + X’Y’Z

= XZ(Y + Y’) + X’Y’Z

= XZ.1 + X’Y’Z

= XZ + X’Y’Z      

= Z (X + X’Y’)

= Z (X + X’)(X + Y’)

= Z.1 (X + Y’)     

= Z (X + Y’)

= ZX + ZY’

= XZ + Y’Z

This the minimized form of the Boolean function F.

Example 2:- Minimize the Boolean function F = X’Z’ + Y’Z’ + YZ’ + XY?

Solution:-

F

= X’Z’ + Y’Z’ + YZ’ + XY

= X’Z’ + Z’(Z’ + Z) + XY

= X’Z’ + Z’(Z + Z’) + XY

= X’Z’ + Z’.1 + XY

= X’Z’ + Z’ + XY

= X’Z’ + Z’.1 + XY

= Z’ (X’ + 1) + XY

= Z’.1 + XY

= Z’ + XY

This is the required minimized result of the function.

Example 3:- Minimize the following algebraic expression F = A’B + ABC’ + ABC?

Solution:-

F

= A’B + ABC’ + ABC

= A’B + AB(C + C’)

= A’B + AB.1

= A’B + AB

= B (A’ + A)

= B(A + A’)

= B.1

= B

Hence this is the required result of the Boolean function.

Canonical Forms of Boolean Function

A Boolean function specified by a truth table can be expressed algebraically in many different ways. Two ways of forming Boolean expression are canonical and non-canonical forms.

Canonical Forms

Canonical forms express all binary variables in product (AND) or sum (OR) term of the Boolean function. There are two types of canonical forms of a Boolean function. The first one is called sum-of-product and the second one is called product-of-sum.

A’BC + A’BC’ + ABC’ + AB’C’ + A’B’C’ + ABC is a canonical sum-of-product form of a Boolean function, the given function has contained three inputs that means three binary variables. In each term of the given function has contained three variables.  (X’ + Y + Z).(X + Y’ + Z).(X’ + Y + Z).(X’ + Y + Z’) is a canonical product-of-sum form of a Boolean function.

Non-canonical forms

A non-canonical form does not express all binary variables in every product or sum term of the Boolean function.

Minterms and Maxterms

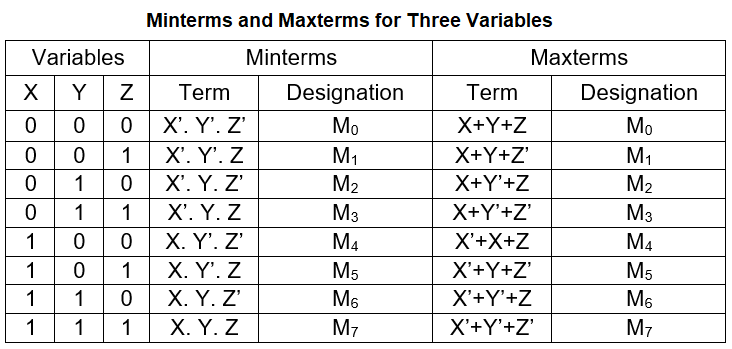
A binary variable may appear either in its normal form (X) or in its complement form (X’). Now consider two binary variables X and Y combined with an AND operation. These two variables can appear in these four possible combinations X’Y’, X’Y, XY’, and XY. Each of these four AND terms is called a minterm or a standard product.

In a similar manner, n variables can be combined to form 2ⁿ minterm. The 2ⁿ different minterms may be determined by a method similar to the one shown below for three variables. The binary numbers from 0 to 2ⁿ – 1 are listed under the n variable.

Each minterm is obtained from an AND term of the n variables, with each variable being primed if the corresponding bit of the binary number is 0 and unprimed if it is 1.

In a similar fashion, n variables forming an OR term, with each variable being primed or unprimed, provide 2ⁿ possible combinations called Maxterms or standard sums. The eight Maxterms for three variables, together with their symbolic designation, are listed below.

Any 2ⁿ Maxterms for n variables may be determined similarly. Each Maxterm is obtained from an OR term of the n variables, with each variable being unprimed if the corresponding bit is 0 and primed if it is 1.

Sum of Product

A sum-of-product expression is a product term (minterm) or several product terms (minterms) logically added together. The following steps are used to express a Boolean function in its sum-of-product form:

1. Construct a truth table for the given Boolean function.
2. Form a minterm for each combination of the variables which produces a 1 in the function.
3. The desired expression is the sum (OR) of all the minterms obtained in step 2.

For example: 011, 100 and 111 their corresponding minterms are X’.Y.Z, X.Y’.Z’, X.Y.Z. Hence, taking the sum of all these minterms, the given function can be expressed in its sum-of-product form as:

F₁ = X’.Y.Z + X.Y’.Z’ + X.Y.Z

F₁ = m₃+m₄+m₇

Similarly, F₂ = X’.Y.Z + X.Y’.Z + X.Y.Z’ + X.Y.Z can be easily expressed in its sum-of-product form:

F₂ = X’.Y.Z + X.Y’.Z + X.Y.Z’ + X.Y.Z

F₂ = m₃+m₅+m₆+m₇

X	Y	Z	F1	F2
0	0	0	0	0
0	0	1	0	0
0	1	0	0	0
0	1	1	1	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

This is the truth table for F₁ and F₂. It is sometimes convenient to express a Boolean function in its sum-of-product form. If not in this form, it can be made. So by first expanding the expression into a sum of AND terms. Each term is then inspected to see if it contains all the variables. If it misses one or more variables, it is ANDed with an expression of the form (X+X’), where X is one of the missing variable. Let us take an example, express the given Boolean function into its sum-of-product form.

F = A’.(B+C’)

F = A’.B+A’.C’

The given function has three variables A, B, and C. The first term of the function A’B is missing one variable, therefore

A’B = A’.B.(C+C’)

A’B = A’.B.C+A’B.C’

Similarly, the second term of the function A’C’ is missing one variable, therefore

A’.C’= A’.C’.(B+B’)

A’.C’ = A’.C’.B+A’.C’.B’

So by combining all the terms we get

F = A’.B.C+A’.B.C’+A’.C’.B+A’.B’.C’

F = A’.B.C+A’.B.C’+A’.B.C’+A’.B’.C’

But in the above expression, the term A’.B.C’ appears twice and according to Boolean postulate we have X+X’ = X. Hence it is possible to remove one of them.

F = A’.B.C+A’.B.C’+A’.B’.C’

Rearranging the minterms in ascending order, we finally obtain:

F = A’.B’.C’+A’.B.C’+A’.B.C

F = m₀+m₂+m₃

F (A, B, C) = ∑ (0, 2, 3)

The summation symbol ‘∑’ stands for the ORing of terms. The numbers following it are the minterm of the function.

Product of Sum

A product-of-sum expression is a sum term (maxterm) or several maxterms logically multiplied (ANDed) together. For example, the expression (X’+Y)(X+Y’) is a product-of-sum expression. The following steps are used to express a Boolean function in its product-of-sum form:

1. Construct a truth table for the given Boolean function.
2. Form a maxterm for each combination of the variables which produces a 0 in the function.
3. The desired expression is the sum (AND) of all the maxterms obtained in step 2.

For example: 000, 010, 011, 101, and 110. The following five combinations of the variable produce a 0.

Their corresponding maxterms are: (X+Y+Z), (X+Y’+Z), (X+Y’+Z’), (X’+Y+Z’), and (X’+Y’+Z). If taking the product (AND) of all these maxterms, we can write them as

F = (X+Y+Z).(X+Y’+Z).(X+Y’+Z’).(X’+Y+Z’).(X’+Y’+Z)

F = M₀.M₂.M₃.M₅.M₆

Let us take an example:-Express the Boolean function in the product-of-sum form.

F = X.Y+X’.Y

At first convert the function into OR term using the distributive law;

F = X.Y+X’.Z

= (X.Y+X’).(X.Y+Z)

= (X+X’).(Y+X’).(X+Z).(Y+Z)

= (X+Y’).(X+Z).(Y+Z)

The function has three variables X, Y, and Z. Each OR term is missing one variable, therefor:

X’+Y = X’+Y+Z.Z’ = (X’+Y+Z).(X’+Y+Z’) = (X’+Y+Z).(X’+Y+Z’)

X+Z = X+Z+Y.Y’ = (X+Z+Y).(X+Z+Y’) = (X+Y+Z).(X+Y’+Z)

Y+Z = Y+Z+X.X’ = (Y+Z+X).(Y+Z+X’) = (X+Y+Z).(X’+Y+Z)

Combining all the terms and removing those that appear more than one, we finally obtain:

F = (X+Y+Z).(X+Y’+Z).(X’+Y+Z).(X’+Y+Z’)

F = M₀.M₂.M₄.M₅

F (X,Y,Z) = π (0,2,4,5)

The product symbol π denotes the ANDing of the maxterms. The numbers following it are the maxterms of the function.